[Linear Algebra] 6-4.Quadratic Form

Linear Algebra
Author

신호연

Published

February 10, 2023

딥러닝공부방,soohee410님의 블로그을 읽고 정리한 내용입니다.

Quadratic Form

Definition

벡터\({\bf{x}}\)의 이차형식(Quadratic form)은 다음과 같이 정의한다.

Definition of quadratic form
\[\begin{aligned} &Q({\bf{x}}) := {\bf{x}}^TA{\bf{x}}\\ &\text{where } \begin{aligned} &A = A^T \in \mathbb{R}^{n \times n},x \in \mathbb{R}^{n \times 1} \end{aligned} \end{aligned}\]
  • 행렬\(A\)를 이차형식의 행렬(matrix of quadratic form)이라고 하며 symmetric matrix이다.

Example

\({\bf{x}} = [x_1,x_2]^T\) ,\(A = \begin{bmatrix}3 & -2 \\ -2 & 7\end{bmatrix}\)일때, quadratic form을 구해보자.

\[\begin{aligned} &Q({\bf{x}}) = {\bf{x}}^TA{\bf{x}} = \begin{bmatrix} x_1 & x_2 \end{bmatrix} \begin{bmatrix}3 & -2 \\ -2 & 7\end{bmatrix} \begin{bmatrix} x_1 \\ x_2 \end{bmatrix} = \begin{bmatrix} x_1 & x_2 \end{bmatrix} \begin{bmatrix} 3x_1-2x_2 \\ -2x_1 + 7x_2 \end{bmatrix} = 3x_1^2 -4x_1x_2 + 7x_2^2 \end{aligned}\]

Change of Variable in a Quadratic From

Problem Setting


위의 그림은 이차형식을 좌표계에서 표현한 것이다. 각각의 이차형식에서 원점으로부터 거리가 가장 먼 좌표를 찾아보자.

  • 초록색 quadtratic form의 경우 직관적으로 \(x_2 = 0\)을 대입하여 거리가 가장 먼 좌표를 바로 구할 수 있다.
  • 그러나 빨강색 quadtratic form의 경우 거리가 가장 먼 곳의 좌표를 구하기가 쉽지않다.
  • crossproduct term인 \(4x_1x_2\)가 존재로 인해서 현재의 좌표축을 기준으로 회전된 타원이 존재하기 때문이다.

만약 빨강색 quadratic form이 위와 같이 새로운 축을 기준으로 표현된다면 어떨까?

  • 새로운 축을 기준으로 빨강색 타원은 회전되지 않은 형태이기에
  • cross product항이 제거되어 가장 먼 곳의 좌표를 직관적으로 \(y2=0\)을 대입하여 쉽게 구할 수 있다.
  • 이와 같이 축을 바꿔서 하여 cross product항을 제거하면 최소 또는 최대가 되는 좌표를 바로 보다 쉽게 구할 수 있게 해줘서 최적화 관점에서 이점이 많다.

그렇다면 주어진 식을 새로운 축을 기준으로 간다하게 바꾸려면 어떻게 해야 뭘까?

  • 이는 이차형식의 변수변환을 활용하면 된다.

Method

  • 이차형식의 변수변환에서 \(\bf{x}\)는 \(\bf{{\bf{y}}}\)와 대칭행렬 \(A\)의 고유벡터의 모음인 \(P\)의 곱이라고 가정한다.
  • 이때 \(P\)는 행렬\(A\)가 대칭행렬이며 따라서 직교대각화가 가능하므로 \(P\)는 \(P^{-1} = P^T\)를 만족하는 orthonormal matrix이다.
    • \(A=A^T\)인 대칭행렬은 직교대각화가 가능하며 고유벡터들은 서로간에 직교한다는 사실을 기억하자.
\[\begin{aligned} &{\bf{x}} = P{\bf{{\bf{y}}}} \\ &{\bf{{\bf{y}}}}=P^{-1}{\bf{x}}\\ &\text{where }P^{-1} = P^T \end{aligned}\]
  • 고유벡터들의 집합인 \(B = \{p_1,p_2,\dots,p_n\}\)를 구성해보자.
  • \(B\)는 \(\mathbb{R}^n\)공간의 표준기저 \(\{e_1,e_2,\dots,e_n\}\)가 아닌 또다른 정규직교기저이다.(B의 span은 \(\mathbb{R}^n\)이기 때문이다.)

그렇다면 여기서 \({\bf{y}}\)는 뭘까?

  • \({\bf{x}}\)를 나타낼 수 있는 정규직교기저이자 \(A\)의 고유벡터 집합인 \(B\)로 표현한 좌표\([{\bf{x}}]_B\)이다.
\[\begin{aligned} &{\bf{x}} = P{\bf{y}}\\ &\Longleftrightarrow {\bf{x}} = p_1y_1 + p_2y_2 + \dots + p_ny_n\\ &\Longleftrightarrow {\bf{y}} = [{\bf{x}}]_B \end{aligned}\]

위에서 가정한 사실을 이차형식에 대입해보자

\[\begin{aligned} &{\bf{x}}^TA{\bf{x}} = (P{\bf{y}})^TA(P{\bf{y}}) = {\bf{y}}^TP^TAP{\bf{y}} = {\bf{y}}^TD{\bf{y}}\\ &\text{where } D = P^TAP,P^T = P^{-1} \end{aligned}\]
  • \(A\)는 symmetric하므로 직교대각화\(D = P^TAP\)가 가능하다.
  • 따라서 벡터\({\bf{x}}\)의 quadratic form은 벡터\({\bf{y}}\)의 quadratic form이 되고
  • \(A\)의 고윳값을 모아놓은 대각행렬 \(D\)가 quadratic form의 matrix가 됨을 알 수 있다.
\[\begin{aligned} {\bf{x}}^TA{\bf{x}}= {\bf{y}}^TD{\bf{y}} = \begin{bmatrix} y_1^T \\ y_2^T \\ \vdots \\ y_n^T \end{bmatrix} \begin{bmatrix} \lambda_1 & 0 &\dots & 0 \\ 0 & \lambda_2 &\dots & 1 \\ \vdots & \vdots &\ddots & \vdots \\ 0 & 0 & \dots & \lambda_n \\ \end{bmatrix} \begin{bmatrix} y_1 & y_2 & \dots & y_n \end{bmatrix} = \lambda_1y_1^2 + \lambda_2y_2^2 + \dots + \lambda_ny_n^2 \end{aligned}\]
  • 조금 더 전개해보면 위와 같은 \(y\)에 관한 식으로 나타난다.
    • 변환결과 \(D\)가 대각행렬이기에 행렬곱의 결과로 crossproduct term이 나타나지 않았으며
    • \(B = \{p_1,p_2,\dots,p_n\}\)를 기저로 하는 새로운 좌표축에서 y에 관한 방정식이 표현되었다.
  • 따라서 원점에서 거리가 가장 먼 지점을 비교적 쉽게 구할 수 있다.
    • \({\bf{y}}^TD{\bf{y}} = \lambda_1y_1^2 + \lambda_2y_2^2\)와 같은 타원이라면
    • $y_2 = 0 $을 대입하여 쉽게 구할 수 있다.
    • 물론 고윳값,고윳벡터를 구하는 과정이 필요함을 잊지말자.

Example : orthogonally diagonalize

\(A =\begin{bmatrix}4 & 2 & 2 \\ 2 & 4 & 2 \\ 2 & 2 & 4\end{bmatrix}\)인 symmetric matrix를 직교대각화해라.

먼저 행렬 A의 고윳값과 고유벡터를 구해보자. 다음과 같은 방정식을 만족하는 \(\lambda\)가 고윳값이다.

\[\begin{aligned} &\text{det}(\lambda I - A) = 0 \\ &\Longleftrightarrow \begin{vmatrix} \lambda -4 & -2 & -2 \\ -2 & \lambda -4 & -2 \\ -2 & -2 & \lambda -4 \end{vmatrix} = 0 \\ &\Longleftrightarrow(\lambda-2)^2(\lambda-8) = 0 \end{aligned}\]

따라서 고윳값은 2와 8이다. 각각의 고윳값에 대한 단위고유벡터를 구해보면 다음과 같다.

  • 이때 \(p_2\)가 바로 구해지지는 않으며 아직 공부하지 못한 방법이다.
  • 서로간에 직교인 고유벡터들을 구성하는 방법은 나중에 공부를 더 해야할 듯 하다.(그람슈미트?직교여공간?)
\[\begin{aligned} & \lambda=2 : p_1 = \begin{bmatrix}-1/\sqrt{2} & 1/\sqrt{2}& 0\end{bmatrix}^T,p_2 = \begin{bmatrix}-1/\sqrt{6}&-1/\sqrt{6}&2/\sqrt{6}\end{bmatrix}^T \\ &\lambda=8 : p_3 = \begin{bmatrix}1/\sqrt{3} & 1/\sqrt{3} & 1/\sqrt{3}\end{bmatrix}^T \end{aligned}\]

대각행렬 D를 구해보면 다음과 같다.

\[\begin{aligned} D = P^{-1}AP = \text{diag}(2,2,8) \end{aligned}\] 
import torch
A = torch.FloatTensor([
    [4,2,2],
    [2,4,2],
    [2,2,4]
])
p_1 = torch.FloatTensor(
    [[-1/2**(1/2),1/2**(1/2),0]]
).T
p_2 = torch.FloatTensor(
    [[-1/6**(1/2),-1/6**(1/2),2/6**(1/2)]]
).T
p_3 = torch.FloatTensor(
    [[1/3**(1/2),1/3**(1/2),1/3**(1/2)]]
).T
P = torch.concat([p_1,p_2,p_3],axis=1)
P_inv = P.inverse()
#대각화
D = P_inv @ A @ P
print("대각행렬 D\n",D.round())
대각행렬 D
 tensor([[2., 0., -0.],
        [-0., 2., -0.],
        [0., 0., 8.]])

Example : Change of Variable in Quadratic Form

위에서 구한 \({\bf{x}} = [x_1,x_2]^T\) ,\(A = \begin{bmatrix}3 & -2 \\ -2 & 7\end{bmatrix}\)일때, quadratic form을 변수변환해보자.

\[\begin{aligned} &Q({\bf{x}}) = {\bf{x}}^TA{\bf{x}} = 3x_1^2 -4x_1x_2 + 7x_2^2 \end{aligned}\]

먼저 고윳값과 고유벡터를 구하면 다음과 같다.

  • 이때 고유벡터는 모두 단위벡터이자 orthonormal한 벡터로 잡자.
\[\begin{aligned} & \lambda=3 : p_1 = \begin{bmatrix}2/\sqrt{5} & -1/\sqrt{5}\end{bmatrix}^T\\ &\lambda=-7 : p_2 = \begin{bmatrix}1/\sqrt{5} & 2/\sqrt{5} \end{bmatrix}^T \end{aligned}\]

대각화를 위해 \(A\)를 대각화시키는 행렬 \(P\)를 구성하자.이때 \(P\)에 대해서 몇 가지를 기억하자.

  • \(P\)는 \(A\)의 고유벡터들을 모아놓은 행렬이자
  • \(P^{-1} = P^T\)를 만족하는 orthonormal matrix이다.(A가 symmetric matrix이기에 가능하다.)

\[P = \begin{bmatrix}2/\sqrt{5} & 1/\sqrt{5}\\-1\sqrt{5} & 2/\sqrt{5}\end{bmatrix}\]

따라서 대각화를 해보면 다음과 같다.

\[D = P^{-1}AP = \begin{bmatrix}3 & 0 \\ 0 & -7\end{bmatrix}\]

이제 위에서 구한 \(P\)로 변수변환을 할 수 있다. \({\bf{x}}\)=\(P{\bf{y}}\)를 quadratic form에 대입해보자.

\[\begin{aligned} Q({\bf{x}}) &= x^TAx = (Py)^TA(Py) = y^TP^TAPy = y^TP^TAPy\\ &=y^TDy = 3y_1^2 - 7y_2^2 \end{aligned}\]

이러한 변수변환을 시각화 해보면 다음과 같다고 한다.

  • x에 대한 quadratic form인 \({\bf{x}}^TA{\bf{x}}\)가 존재하며 그 값은 16이다.
  • \({\bf{x}} = P{\bf{y}}\)를 x에 대한 2차형식에 대입하여 y에 대한 quadratic form으로 변수를 바꿨으며 그 값도 마찬가지로 16이다.
  • \({\bf{x}}^TA{\bf{x}} = {\bf{y}}^TD{\bf{y}} = 16\)으로 같은 값에 mapping됨을 기억하자.(변수변환을 해도 나타내는 형태(타원)는 그대로이다.)

The Principal Axes Theorem

Principal Axes Theorem(주축정리)는 위에서 공부한 사실에 대한 정리이다.

The Principal Axes Theorem

\(A\)가 \(n \times n\)인 대칭행렬일 때, quadratic form인 \(x^TAx\)를 cross-product항이 존재하지 않는 이차형태 \(y^TDy\)로 변환시키는 직교 변수변환 \({\bf{x}} = P{\bf{y}}\)가 존재한다.

(Detail)

  • 이때 \(A\)행렬의 고유벡터는
    1. Orthonormal matrix \(P\)의 각각의 열(column)이며
    2. 새로운 축으로 표현할 때의 정규직교기저이다.
  • Orthonormal matrix \(P\)를 이차형식의 주축(principal axes)라고 부른다.

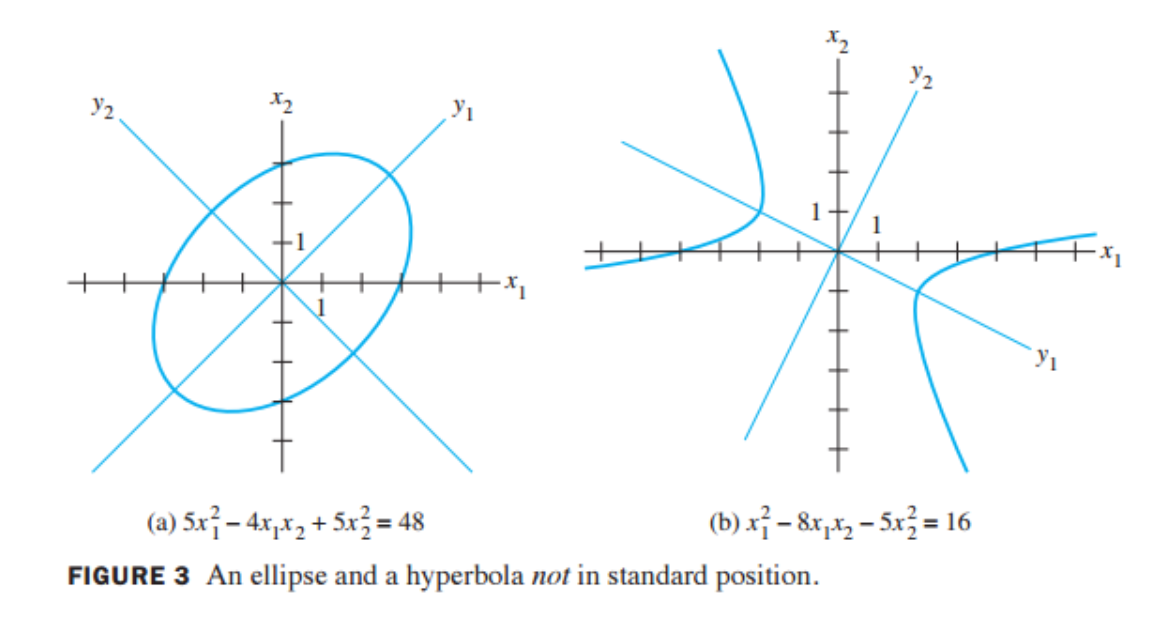
  • 위의 그림의 (a)는 바로 위 예제에서 사용된 이차형식이다.
    • \(y_1\)과 \(y_2\)는 \(\mathbb{R}\)^2의 기저인 \(B = \{p_1,p_2\}\)을 기저로 하는 새로운 축이며
    • 타원은 이 축을 기준으로 원점에 놓이며 회전하지 않은 (표준)형태이다.

Classifiying Quadratic Forms

이차형식의 부호는 다음과 같이 정의할 수 있다.

이차형식의 부호
\[\begin{aligned} &x \not =0,Q(x)>0 \Longleftrightarrow \text{positive definite}\\ &x \not =0,Q(x)<0 \Longleftrightarrow \text{negative definite}\\ &\text{Q(x)가 양수와 음수 모두 지닌다면} \Longleftrightarrow \text{indefinite}\\ &Q(x)\geq 0 \Longleftrightarrow \text{positive semidefinite}\\ &Q(x)\leq 0 \Longleftrightarrow \text{negative semidefinite} \end{aligned}\]

다음과 같은 이차형식을 고려해보자.

\[Q({\bf{x}}) = {\bf{x}}^TA{\bf{x}}\]

주축정리에 의해 어떤 이차형식에 대하여 직교변환이 존재함을 알 수 있다. 이에 따라 전개하면 다음과 같을 것이다.

\[Q({\bf{x}}) = {\bf{x}}^TA{\bf{x}} = {\bf{y}}^TD{\bf{y}}=\lambda_1x_1^2 + \lambda_2x_2^2 + \dots + \lambda_nx_n^2\]

\(x\)에 관한 제곱항은 모두 양수이므로 행렬 \(A\)의 고윳값의 부호에 의하여 이차형식의 부호가 결정된다.

\[\begin{aligned} &\forall i,\lambda_i > 0 \Longleftrightarrow \text{positive definite}\\ &\forall i,\lambda_i < 0 \Longleftrightarrow \text{negative definite}\\ &\forall i,\lambda_i\text{ 가 양수이거나 음수이다.}\Longleftrightarrow \text{indefinite} \end{aligned}\]

\({\bf{x}}^TA{\bf{x}}> 0 \Longrightarrow\) A가 invertible하다.

임의의 행렬 \(A \in \mathbb{R}^{n \times n}\)일 때 다음이 성립한다.

\[\text{det}(A) = \lambda_1\lambda_2\dots\lambda_n\]

만약 \(A = A^T\)인 대칭행렬이며 이차형식이 positive definite라면 다음과 같다.

\[({\bf{x}}^TA{\bf{x}}>0) \Longleftrightarrow \text{positive definite}\rightarrow \forall i,\lambda_i >0 \rightarrow \text{det(A)}>0 \rightarrow A : \text{invertible}\]

\(\therefore\) 이차형식이 positive definite라면 이차형식의 행렬\(A\)는 invertible하다.

참고자료

딥러닝공부방 - [선형대수학] 6.2 이차 형식(Quadratic Forms)
soohee410님의 블로그 - [선형대수] Quadratic Forms, Principal Axes Theorem, Positive Definite Matrix